
円柱の表面積と体積を求める公式 具体例で学ぶ数学
楕円の面積と楕円体の体積の求め方 korokoro 年10月7日 こんにちは( @t_kun_kamakiri )。 さてこの記事を読みに来た方は、「楕円の面積や体積の公式」を求めてきたことだと思います。 あるいは、楕円の面積や体積の公式はどうやって導かれるのかと知り立体の表面積展開図(入試問題) → 携帯版は別頁 == 立体の表面積展開図(入試問題) == 要点11 ≪円柱の側面積≫ 円柱の表面積は,2つの底面積と側面積の和になります. 右図のように底面の半径が r ,高さが h である円柱の側面は長方形で,側
立体の表面積の求め方
立体の表面積の求め方-立体角は、半径1の球(単位球)の一部の面積で定義されていました。単位球の表面積は $4\pi$ なので、立体角は、$0$ 以上 $4\pi$ 以下です。 「$4\pi$ ステラジアン」は「全方位」に対応する立体角です。 立体角の計算例 さっそく、例題の表面積を求めてみよう。 底面が2つ、側面が1つだから、 9π×2 60π = 78π になるね! おめでとう!円柱の表面積の問題を瞬殺できるようになったね!! まとめ:「円柱の表面積の求め方」は公式なんかいらねえ!

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
小学6年生の算数 角柱や円柱の体積の求め方・公式 問題プリント 無料ダウンロード・印刷できる、角柱・円柱の体積を求める練習問題プリント です。 角柱や円柱の名前、体積を求める公式を確認し、体積の計算をする練習を繰り返し行うことができ よって、球面上の表面積がSのときの立体角ωsrは ω=S/R^2・・・① Sm^2球面の表面積、Rm半径 ということになります。 今回の公式を導出するポイントは球の表面積Sm^2 を求めることです。 考え方球の表面積=半径×半径×円周率(314)×4 全国の中学校をお探しの方はこちらへ 全国の中学校 このコンテンツが気に入ったらシェアしてね! 中学校 / 立体の表面積
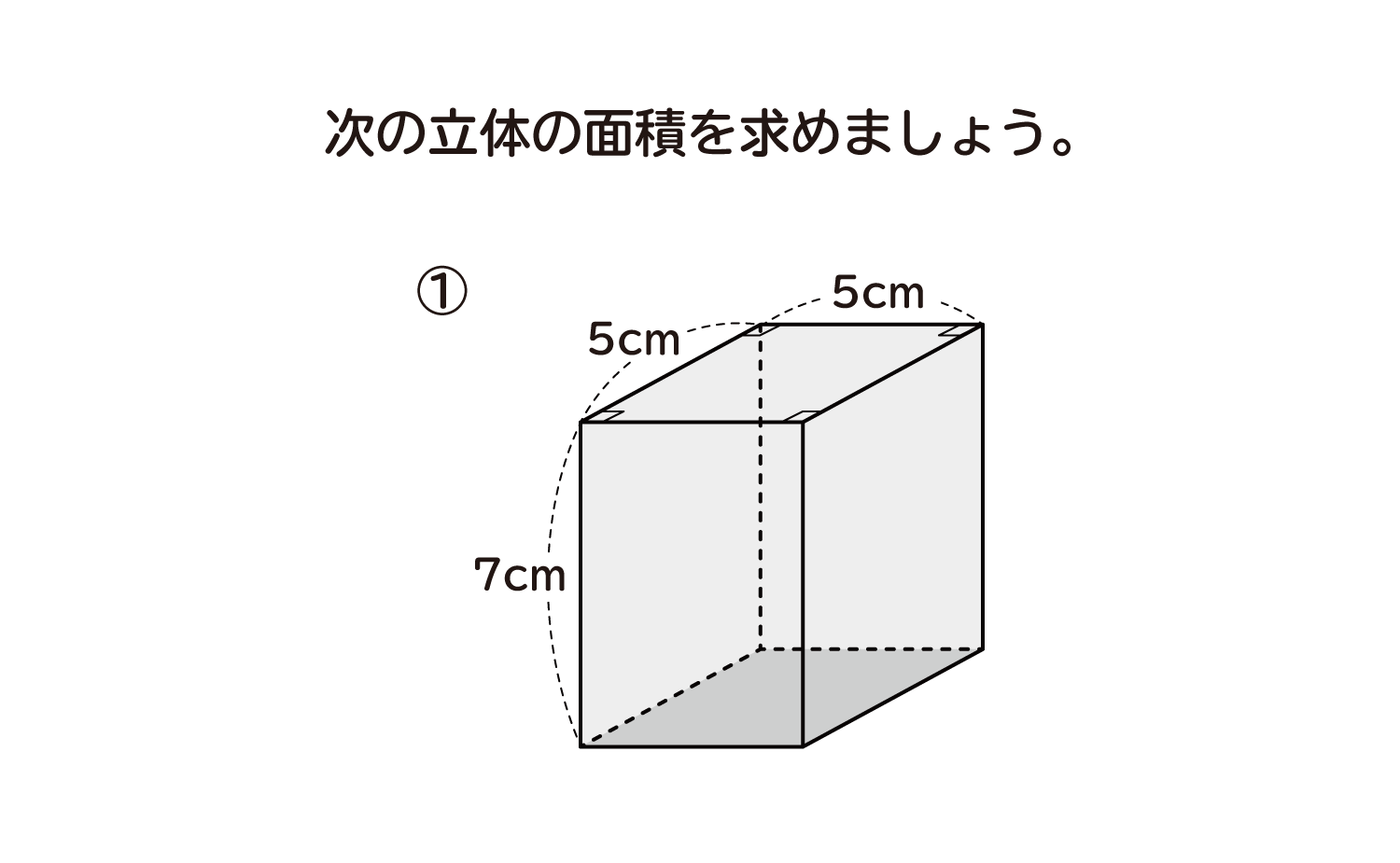
球の表面積 < (2) 2つの比較 (1)(2)より, < 球の表面積 < 方法②:輪切りにする 指針(考え方) この円柱の側面積= 球の表面積の公式と同じ式をしていることが分かる. あなたは今、球の表面積を求める公式を知らないものとします.2角柱と円柱 角柱・円柱の体積=底面積×高さ 角柱・円柱の表面積=底面積×2側面積 3角すいと円すい直方体の表面積の求め方 直方体の表面積は下記の公式で求めます。 a、b、cは直方体の一辺の長さです。下図に直方体を示しました。立方体と違って一辺の長さがそれぞれ異なります。異なる形状の長方形が3つあり6面を構成します。 まとめ
立体の表面積の求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 | 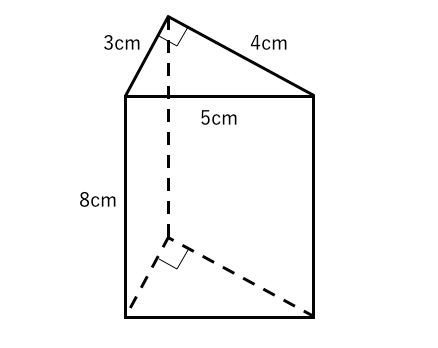 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 | 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 | 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 | 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 | 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 | 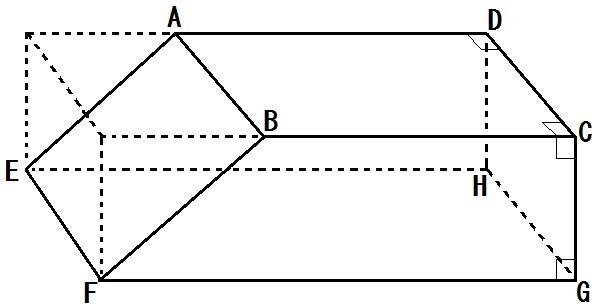 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 | 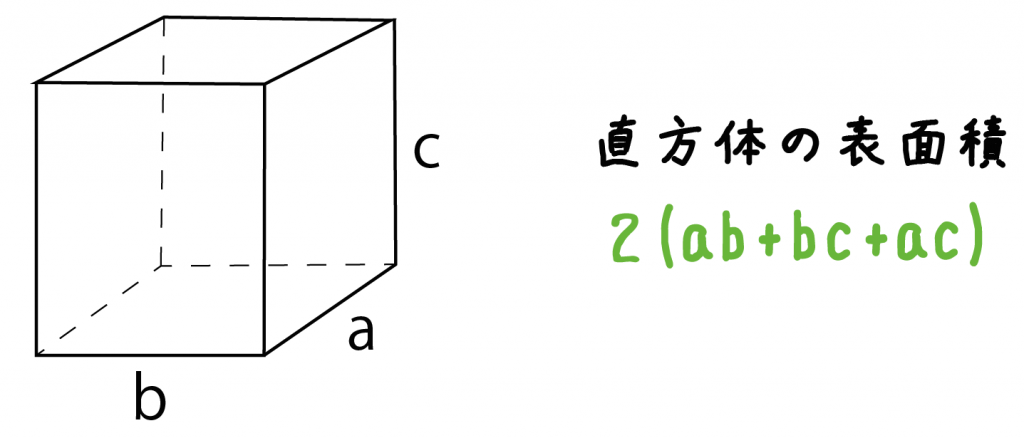 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 | 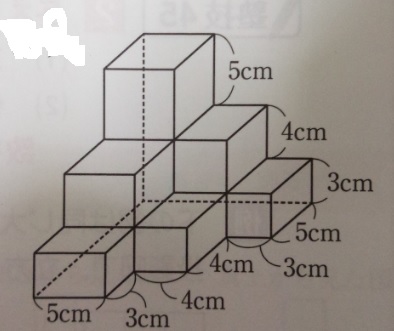 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 | 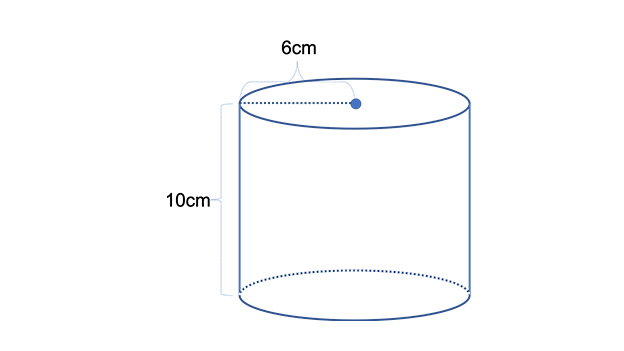 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 | 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 | 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 | 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 | 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 | 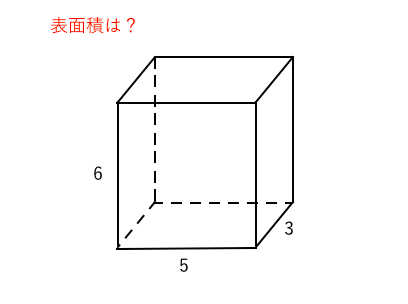 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 | 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
 複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |  複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座 |
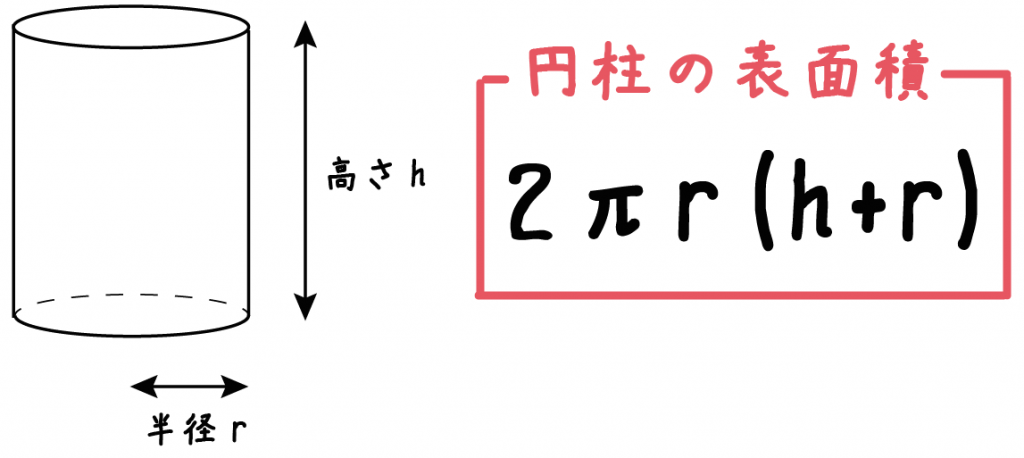
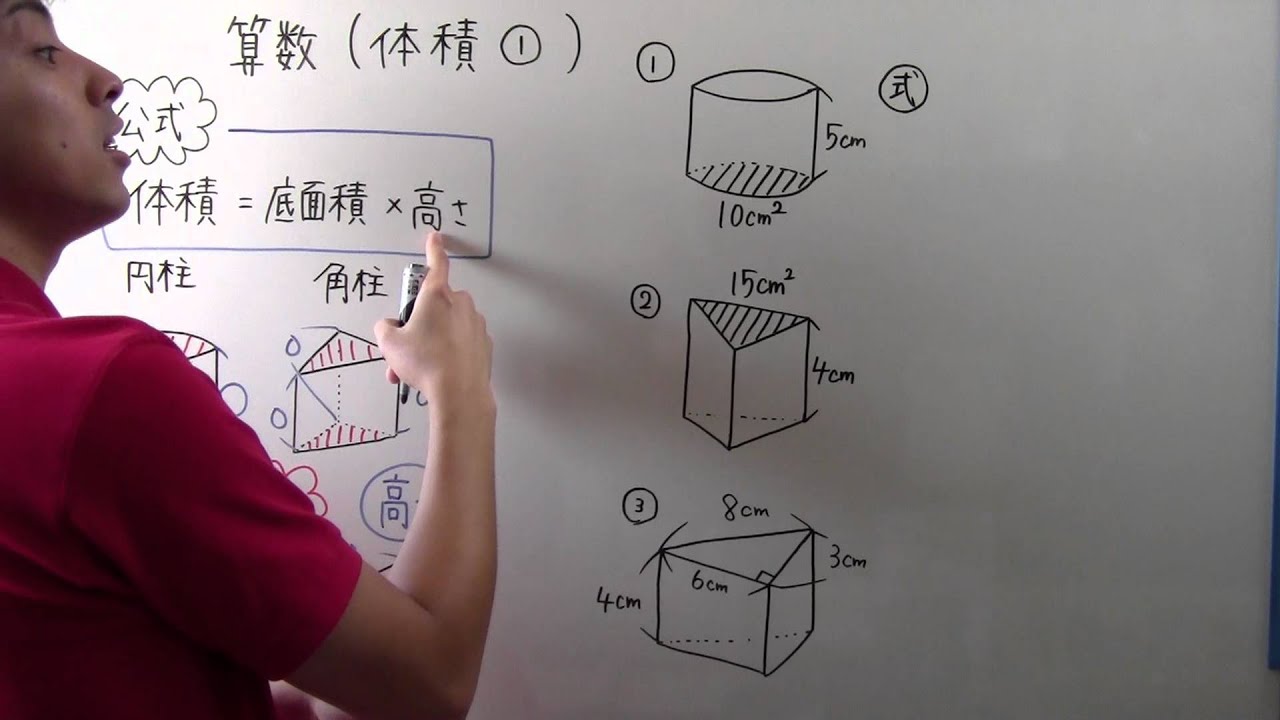
続いて、三角柱の表面積の公式は「底面積 × 2 側面積」でしたね。 すると、底面積は先に求めた$8cm^2$ですね。 側面積の求め方ですが「高さ × 底面の周の長さ」で求めることができます。 底面の周の長さは「5cm,4cm,4cm」と出ているので足して13cm。 今回は立体図形の1つ、円柱の表面積の求め方について書きたいと思います。 円柱の表面積の求め方公式 円柱の表面積を求めるときには展開図をイメージ 円柱の表面積を求める問題 問題① 《円柱の表面積の求め方》 問題② 《円柱の表面積の求め方》 問題③ まとめ スポンサードリンク
Incoming Term: 立体の表面積の求め方, 立体の表面積の求め方 公式,



