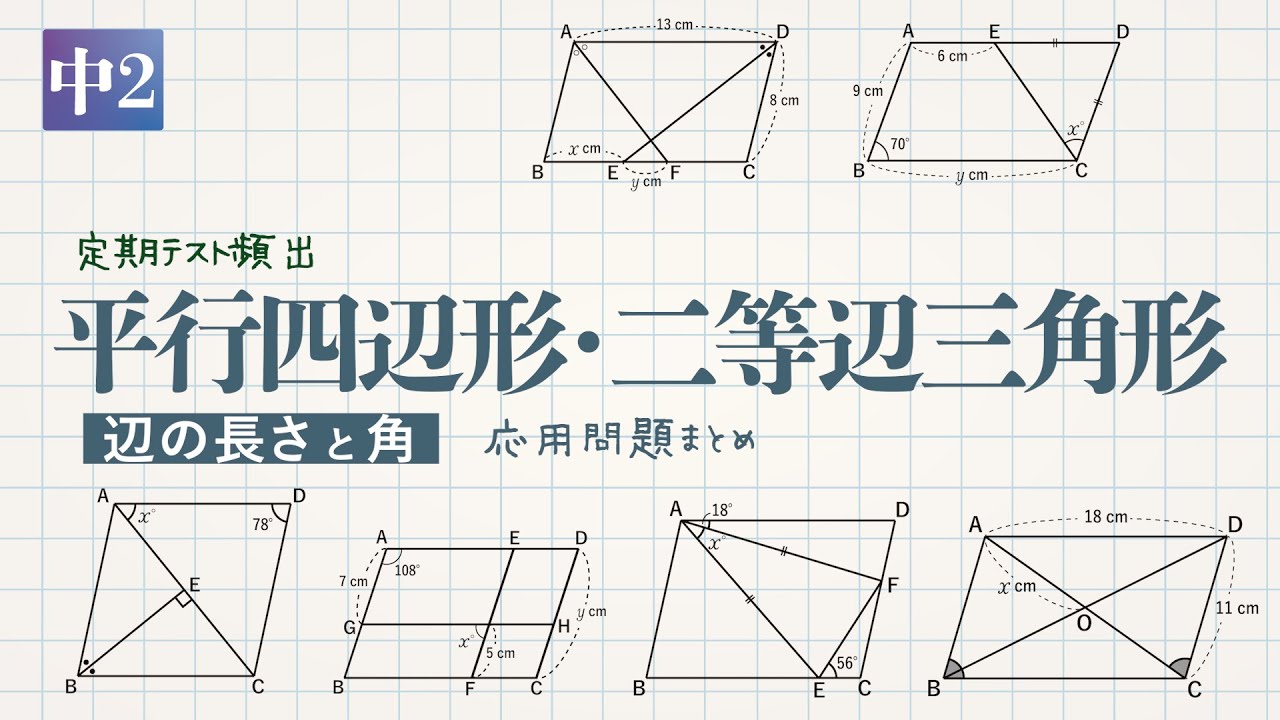
中2 三角形と四角形 平行四辺形 二等辺三角形の辺の長さと角 応用問題まとめ デジタル板書データ Youtube
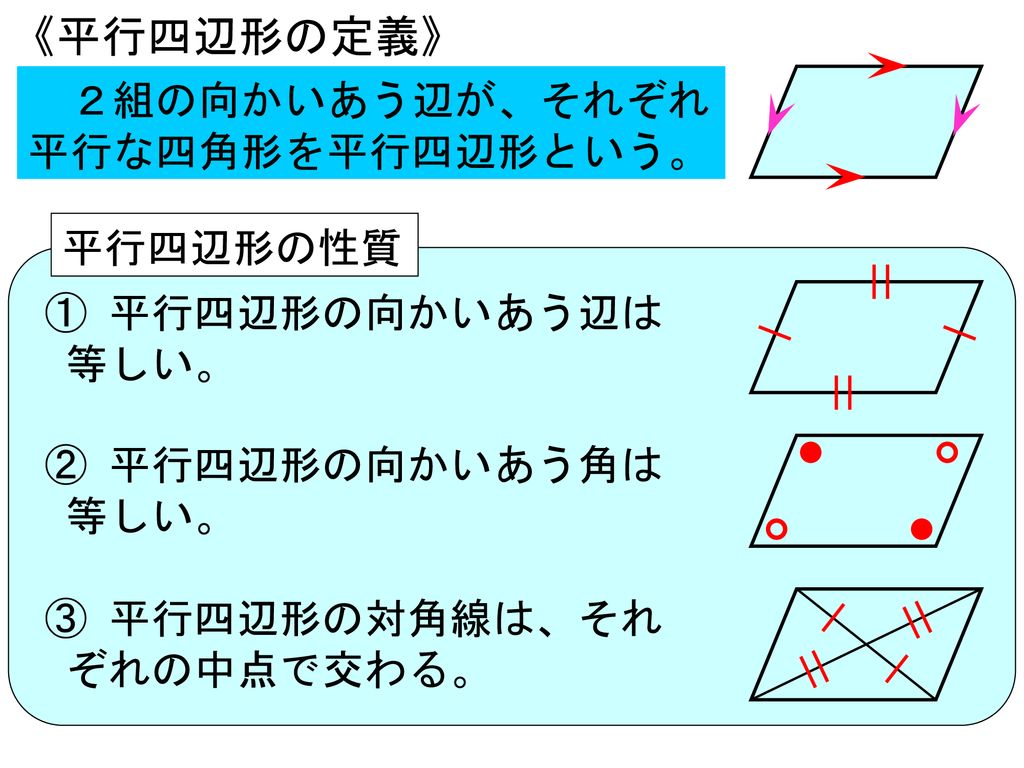
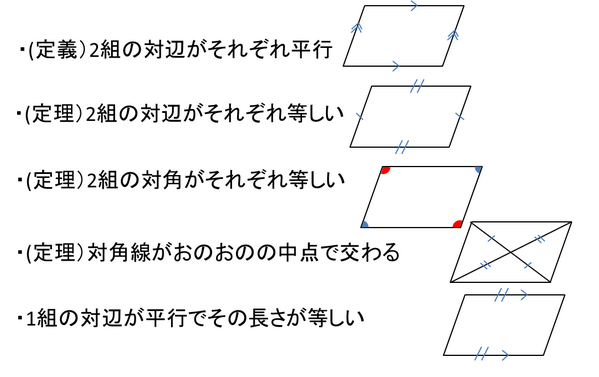
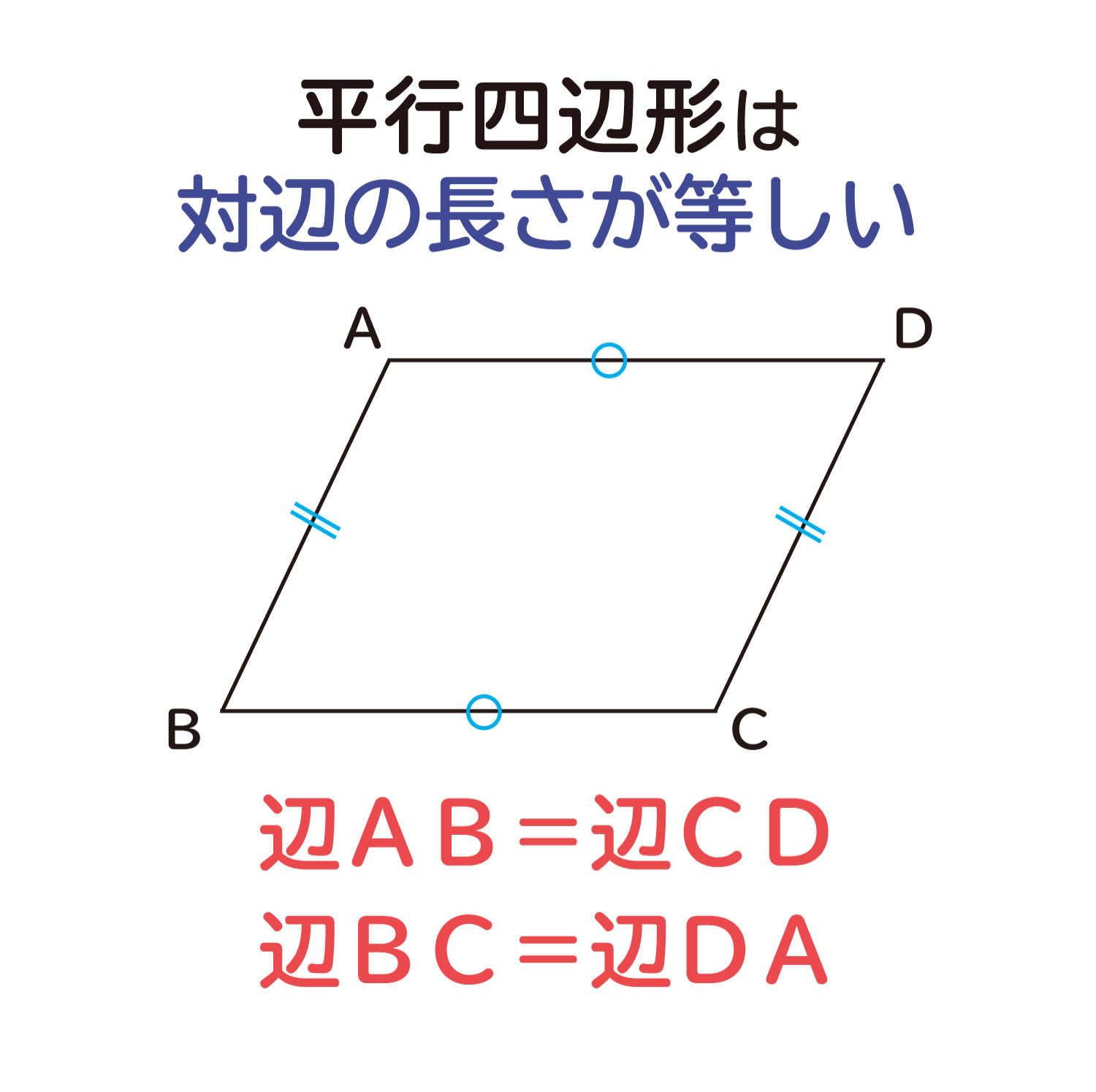
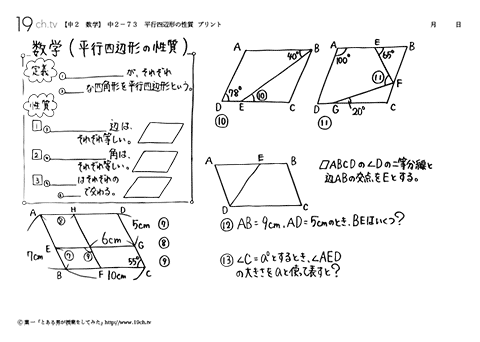
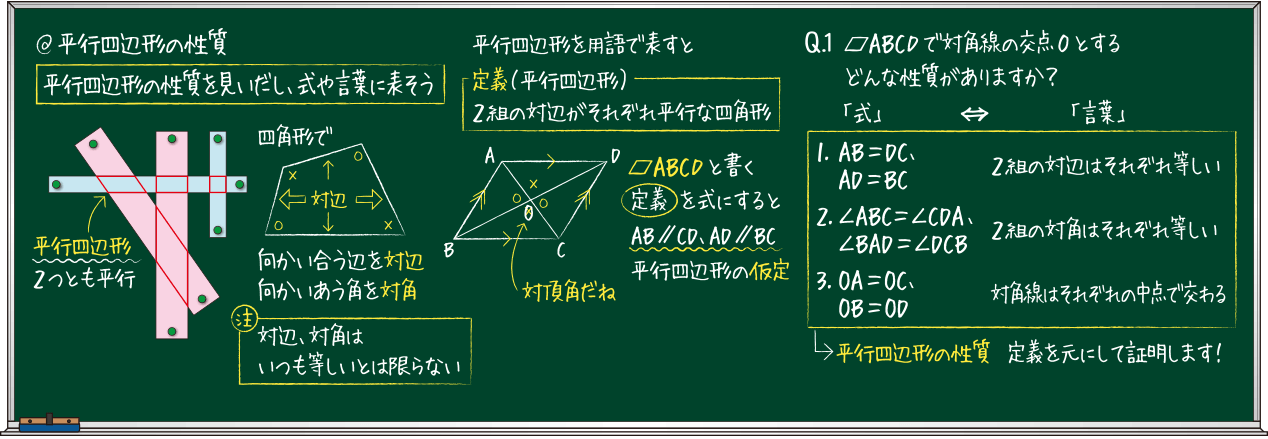
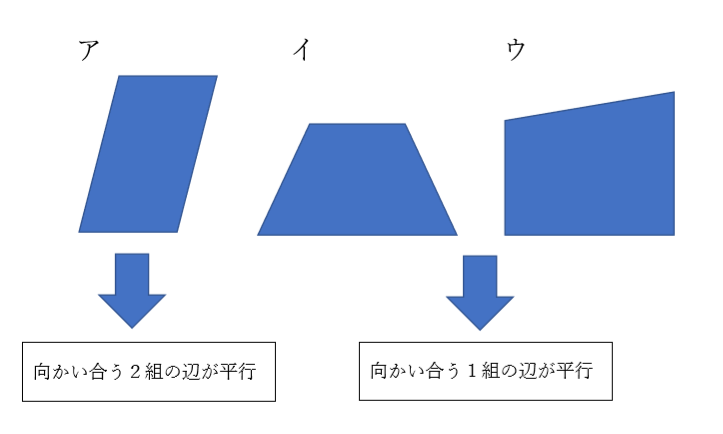
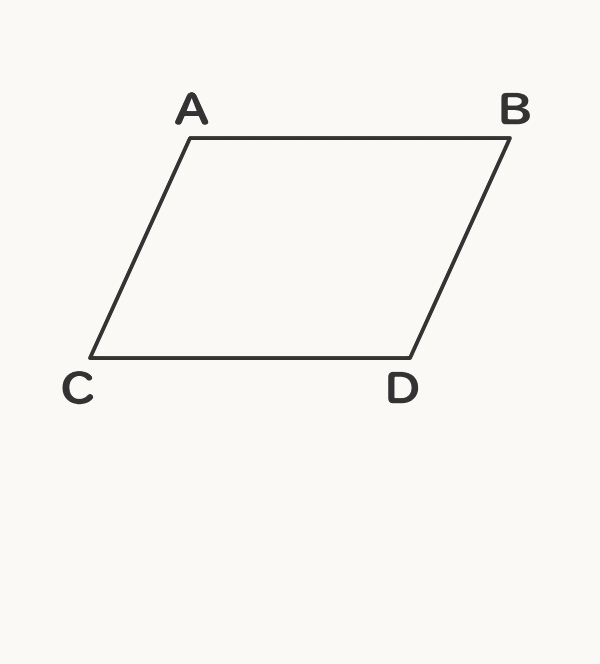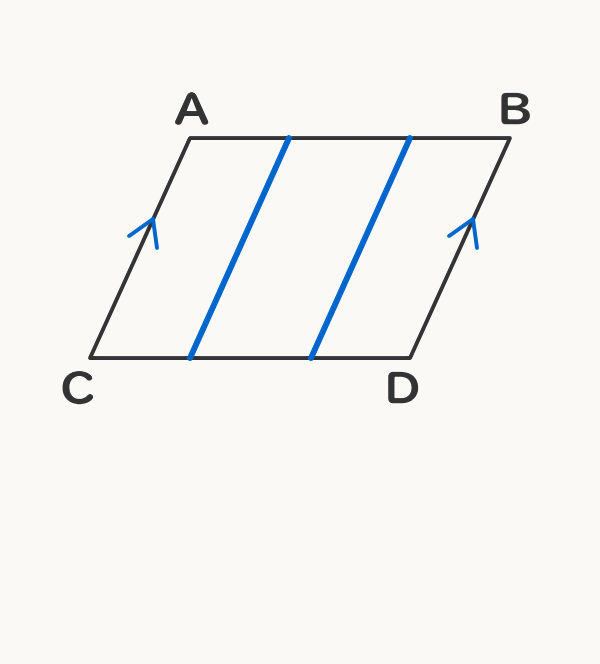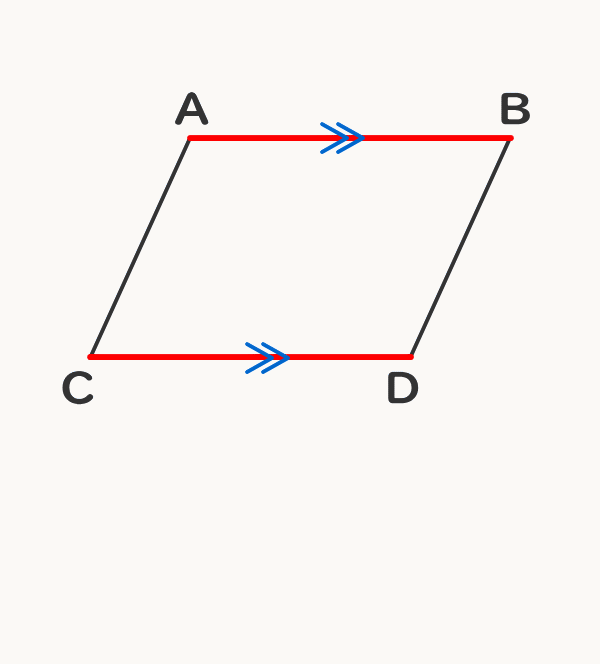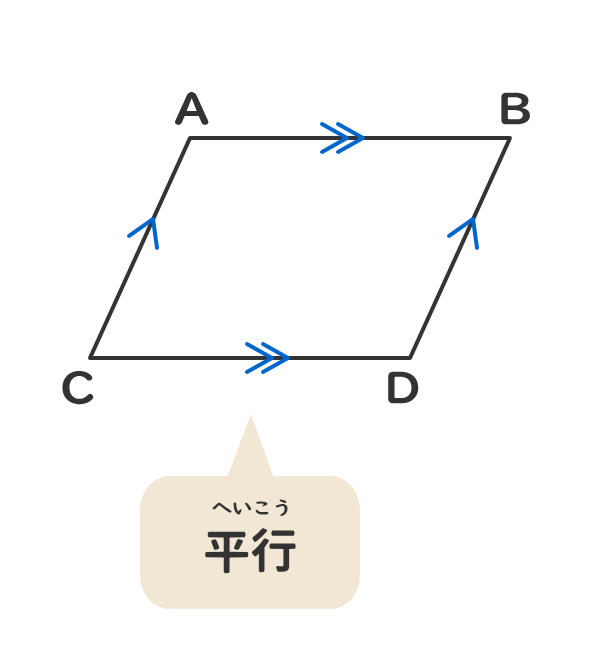
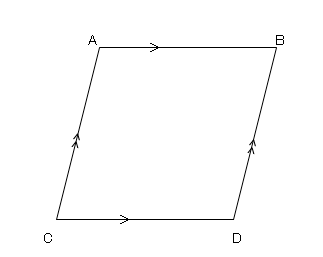
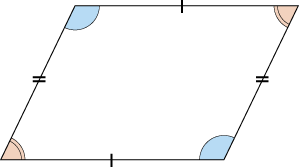
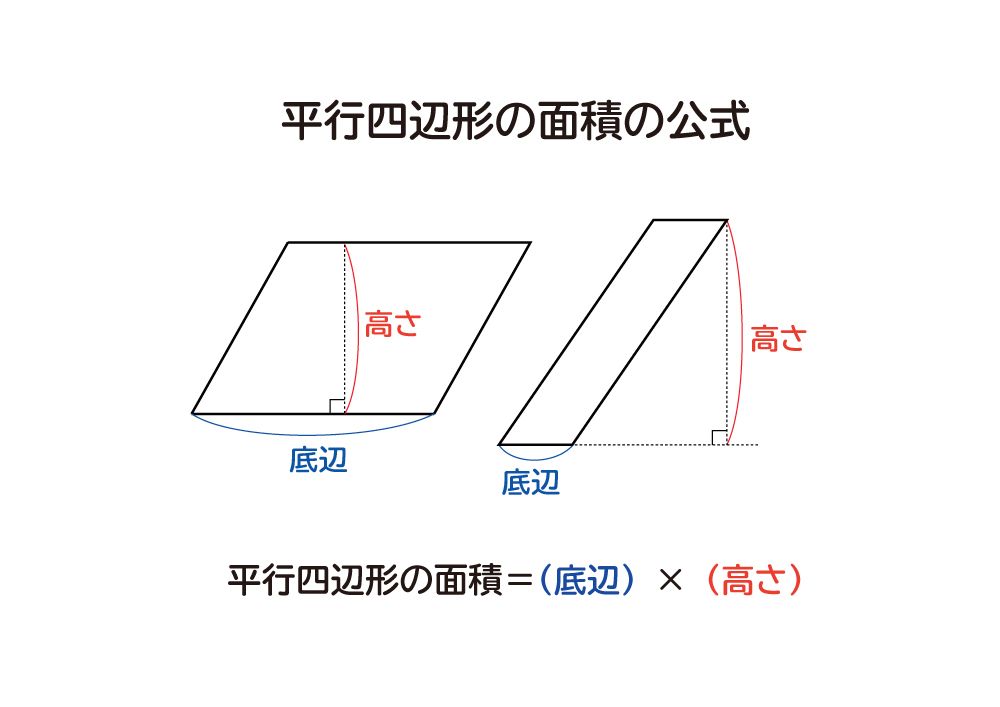
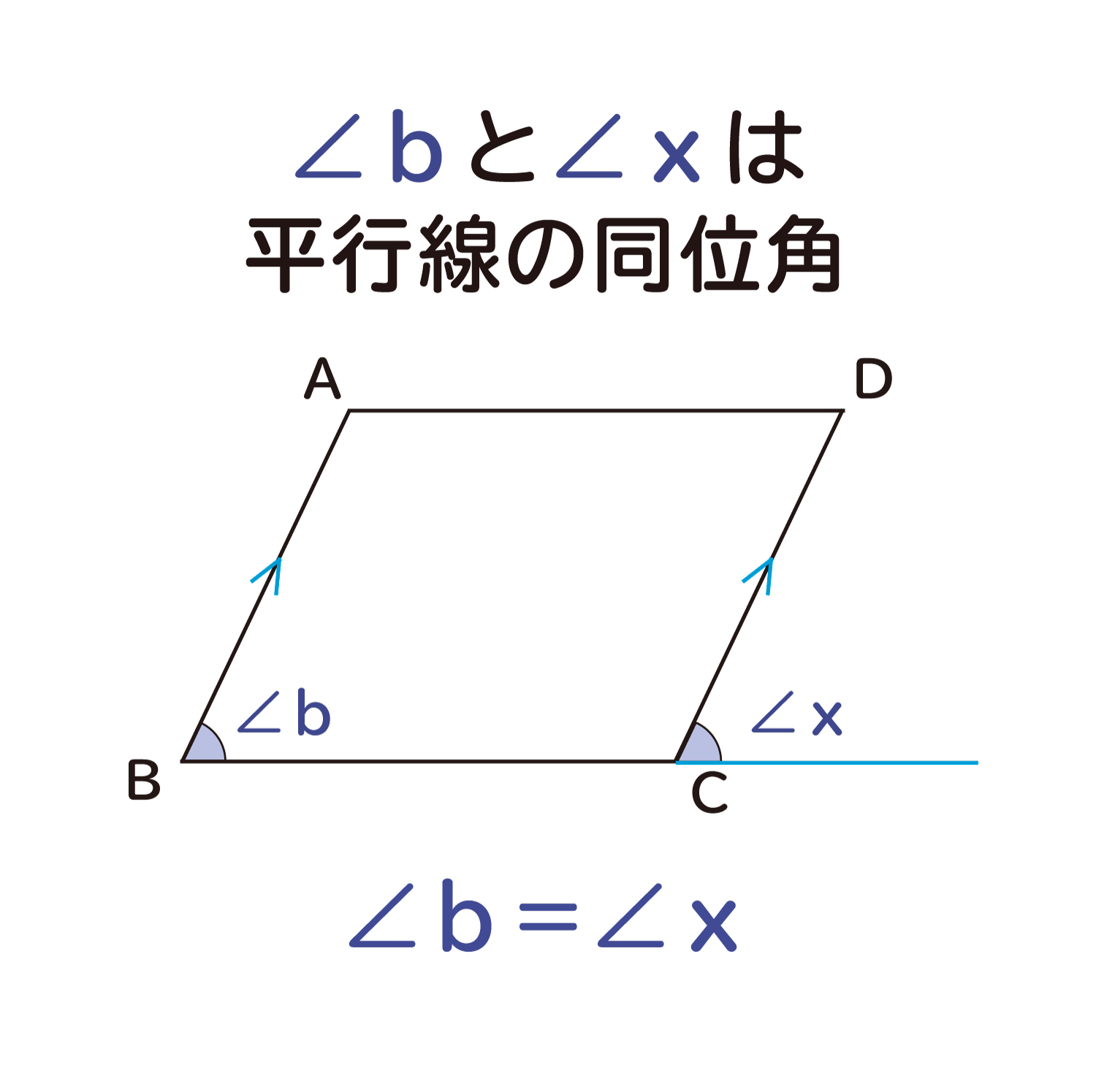
「平行四辺形の定義」 2組の対辺がそれぞれ平行である四角形 「性質」 :平行四辺形と呼ばれるものには 共通してこんなことが言えるね! 「定理」 :性質の中で特に大切なこと! だから証明はいらないよ! こんな感じです。 例えば、コーラ。 定義:黒くてシュワっとする飲み物 性質 平行四辺形の定義2組の対辺が平行な四角形を平行四辺形といいます。平行四辺形の性質平行四辺形は以下のような性質があります。1 2組の対辺の長さが等しい2 2組の対角の大きさが等しい3 2つの対角線はそれぞれの中点で交わる平行四辺形の性質の証明平行四辺形の定義を利用して性質を
平行四辺形の定義は
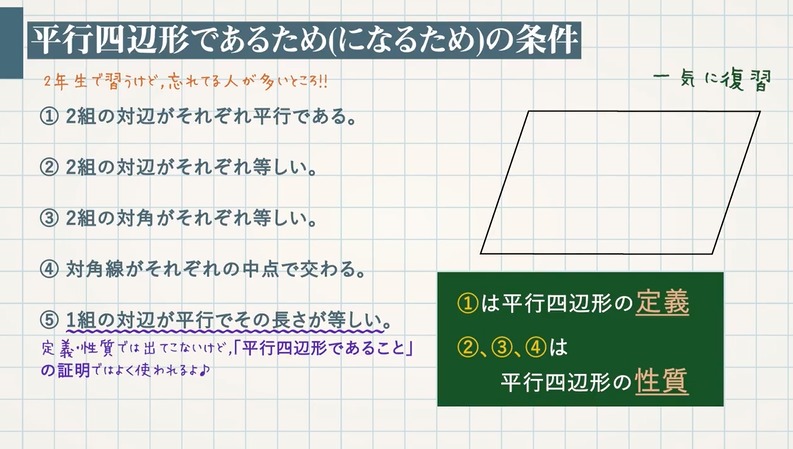
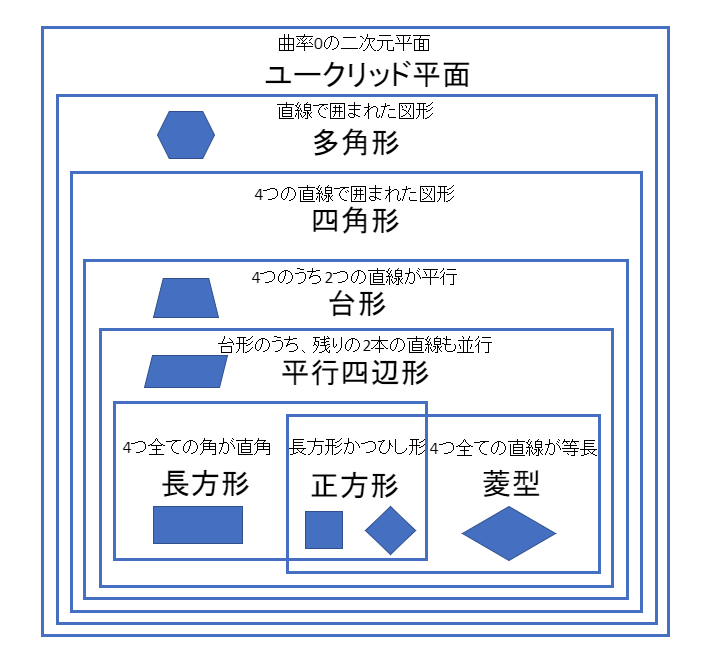
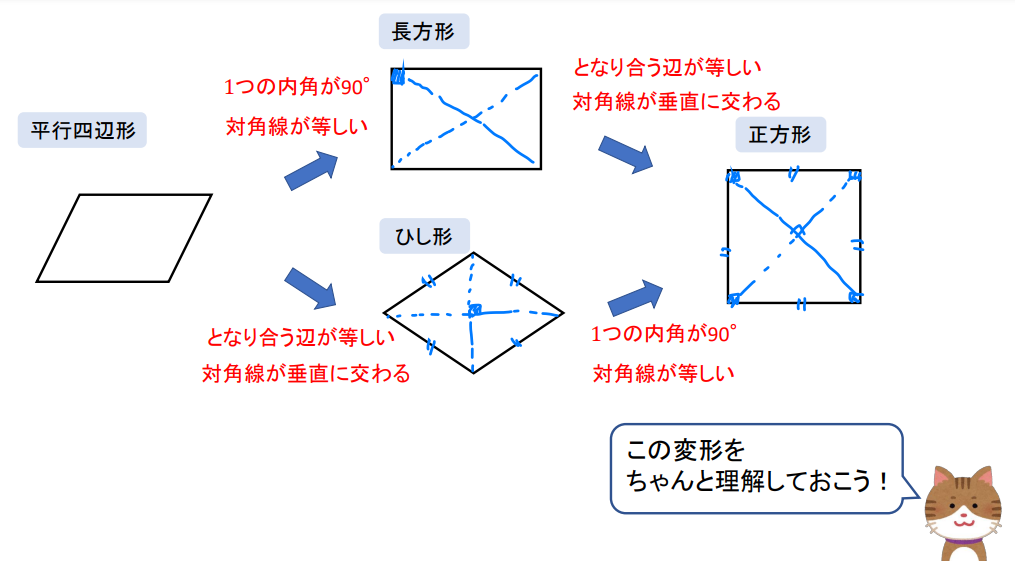
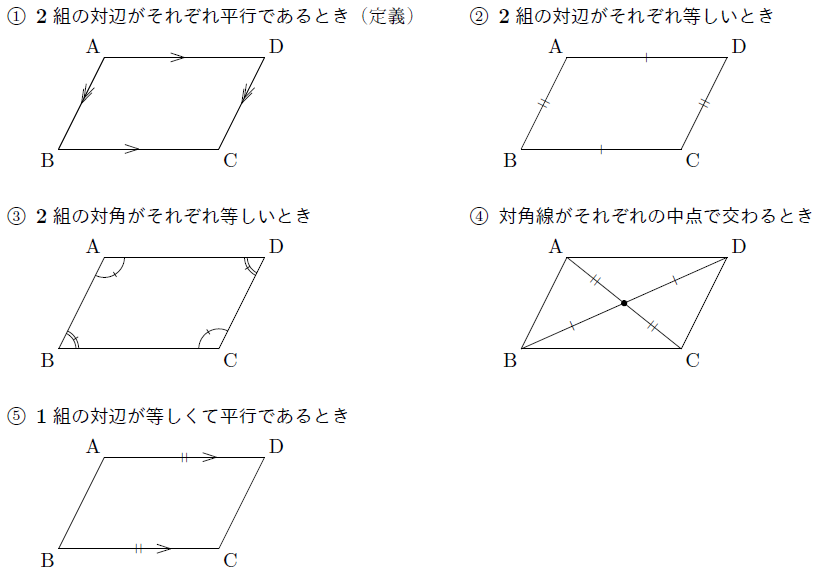
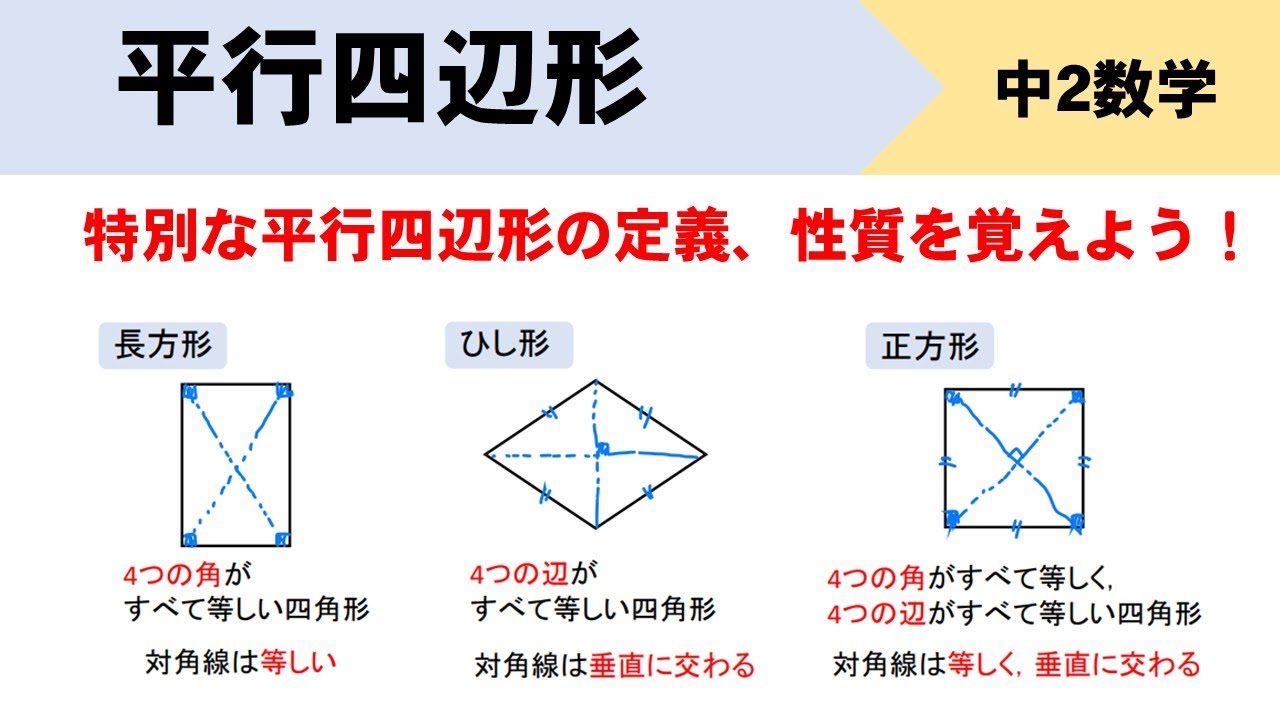
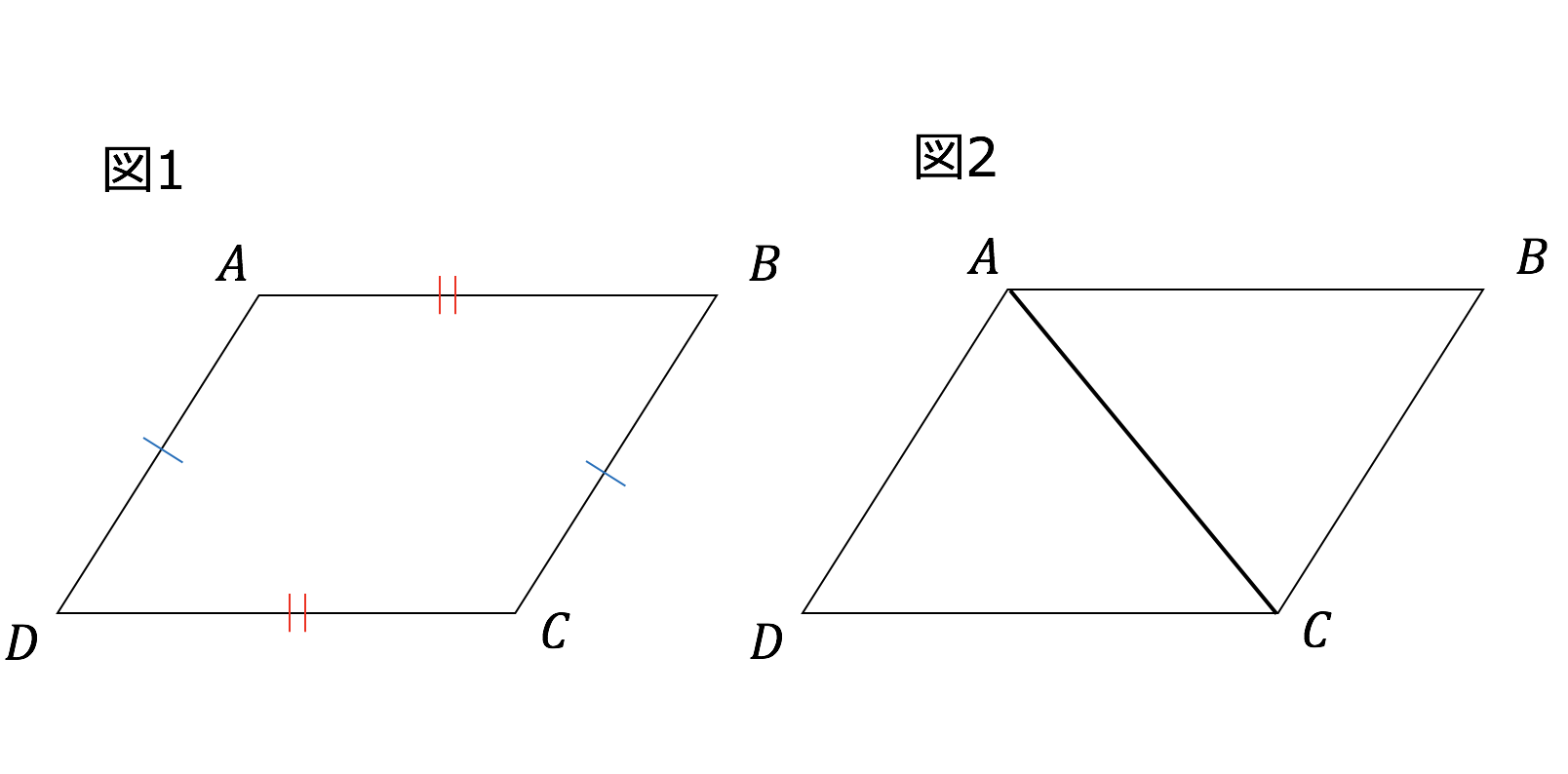
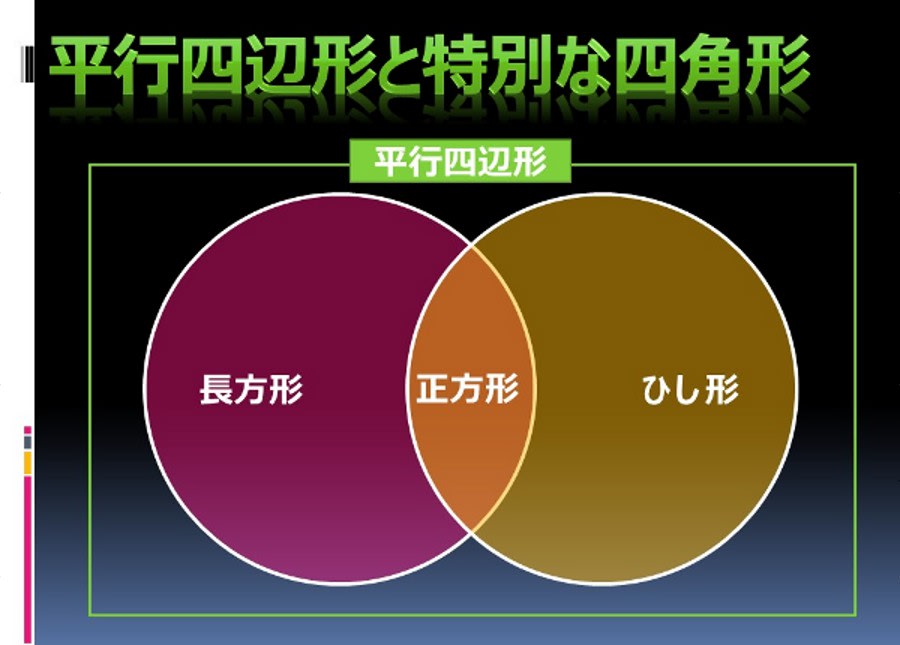
平行四辺形の定義は-特別な平行四辺形の定義、性質を覚えよう! これまでに学習してきたように、平行四辺形とは2組の対辺が平行である四角形のことでしたね。 参考平行四辺形の角度、辺の長さ求め方を問題解説! そして、この平行四辺形をもっと細かく分類すると次のようになります。 平行四辺形の 今回は中2数学で学ぶ、平行四辺形になる条件について勉強したいと思います。 平行四辺形になる条件 2組の対辺がそれぞれ平行である 2組の対辺がそれぞれ等しい 2組の対角がそれぞれ等しい 対角線がそれぞれの中点で交わる 1組の対辺が平行で等しい 平行四辺形であることの証明問題 問題①
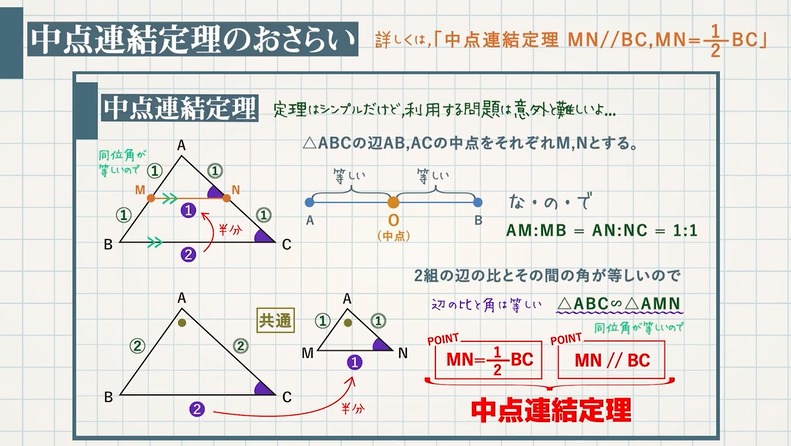
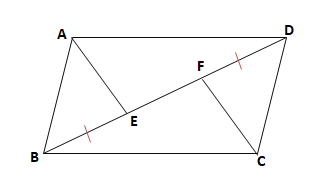
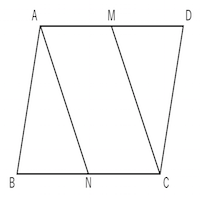
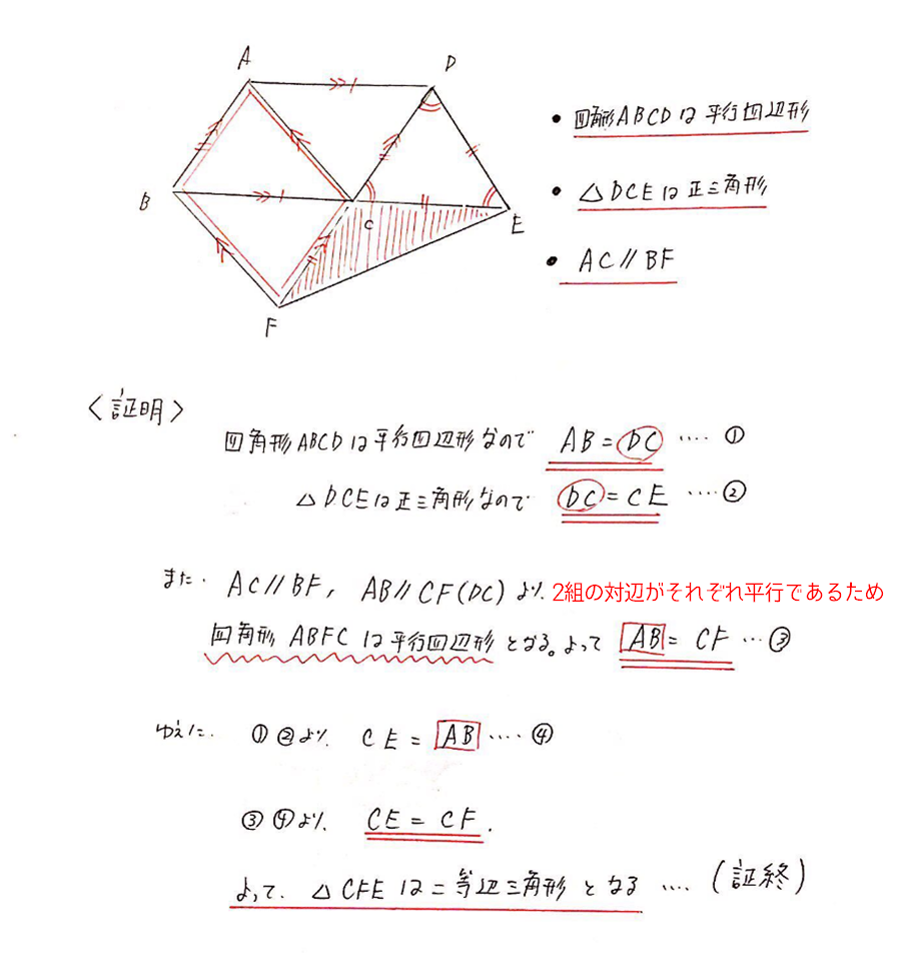
中点連結定理を使った平行四辺形であることの証明 教遊者
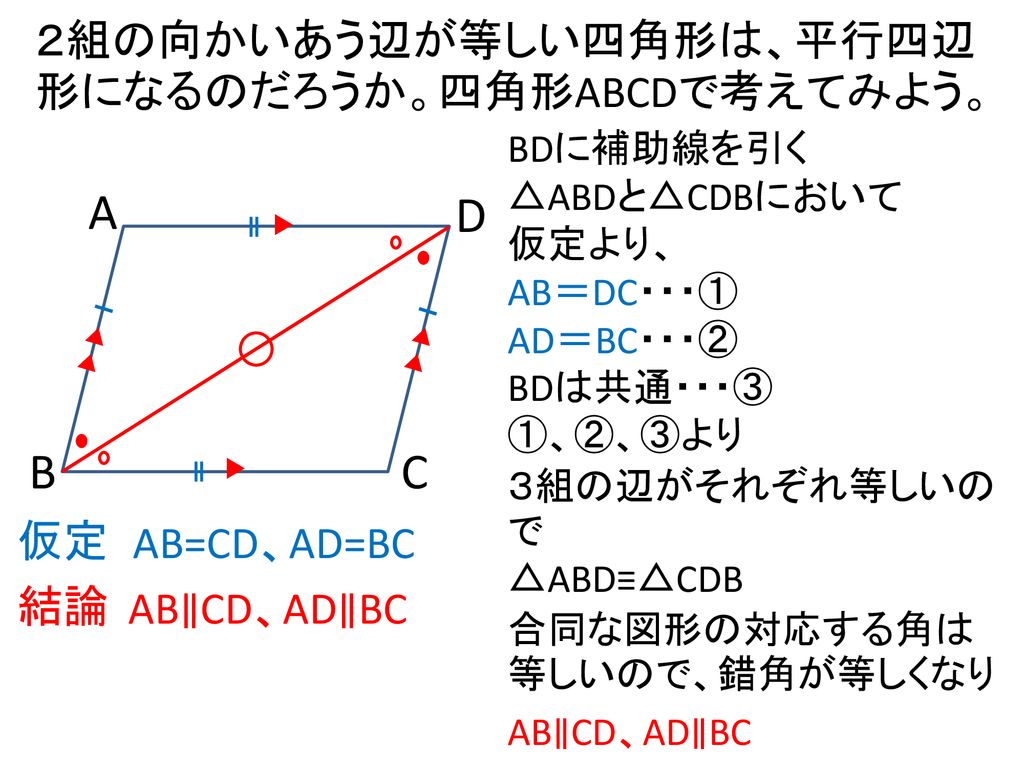
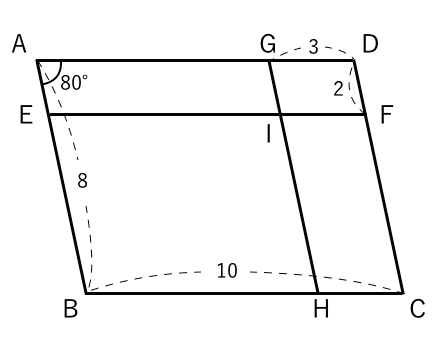
定義は「こういう四角形を平行四辺形としよう」と決めたことなので、これを証明することはできません。 「なぜ平行四辺形の向かい合う2組の辺は平行なのか?」と問われたら、 「そのような四角形が平行四辺形と定義されているから」 という答えになってしまいます。平行四辺形になるための, 上の条件1~5を,記号で表しなさい。 2 四角形abcdが,平行四辺形となる場合は を,ならない場合は×を,( )にかきなさい。 また,なる場合はその条件を言葉でかきなさい。(ただし,図は正確ではない) (1) 条件1定義の逆 「ひし形」 とは、 「4つの辺が等しい四角形」(定義) のことですね。そして、ひし形は平行四辺形の一種ですから、 「平行四辺形の定義・性質」 は全て合わせ持った上で、 「対角線が直交する」 という特質を持っていますね。 では、どのような条件が揃えば、その図形は「ひし形」と言え
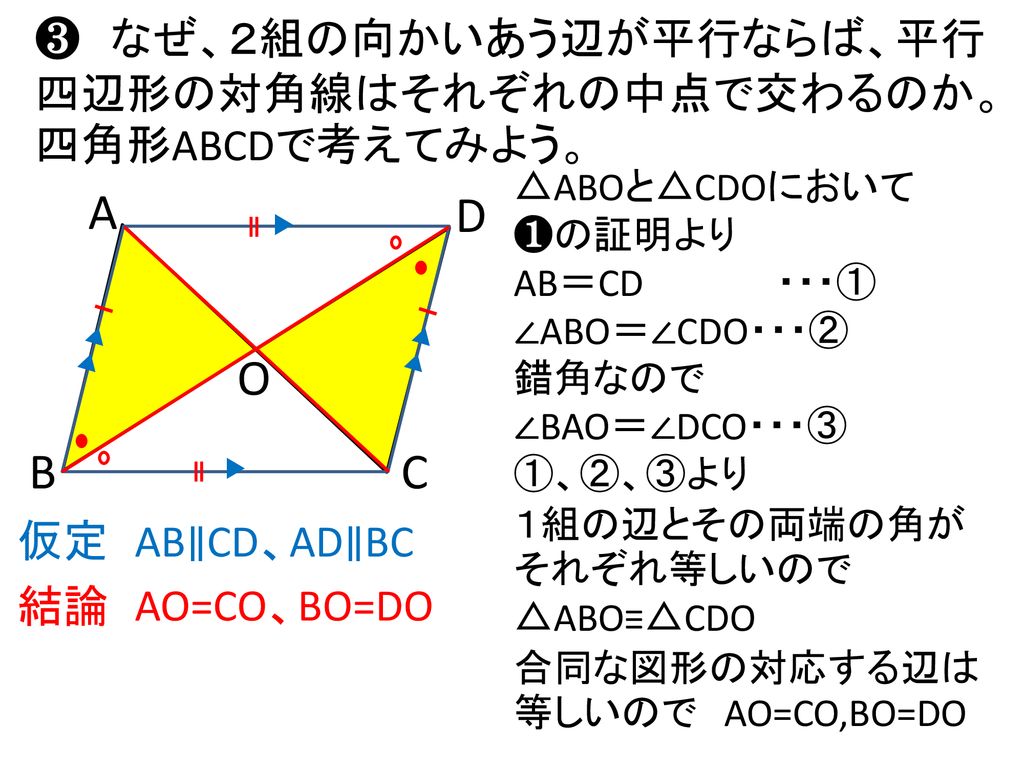
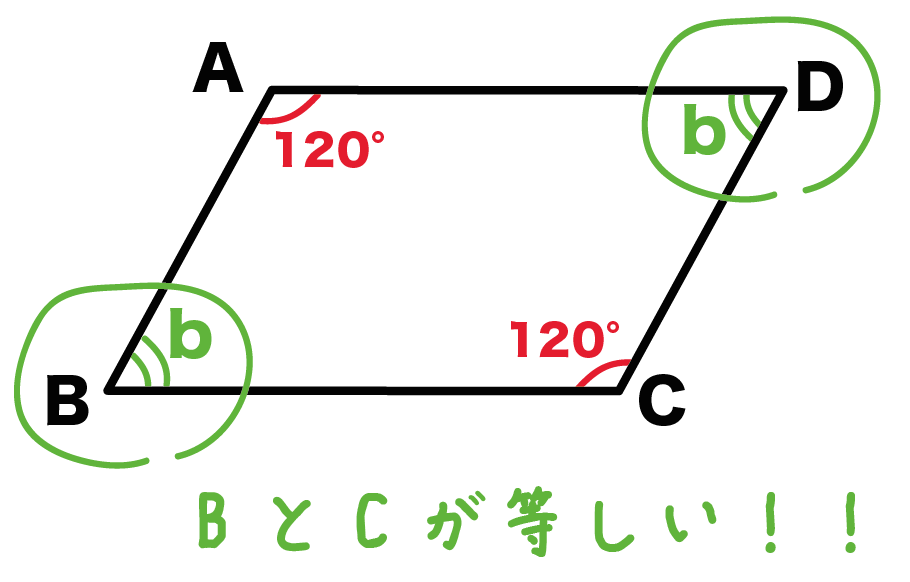
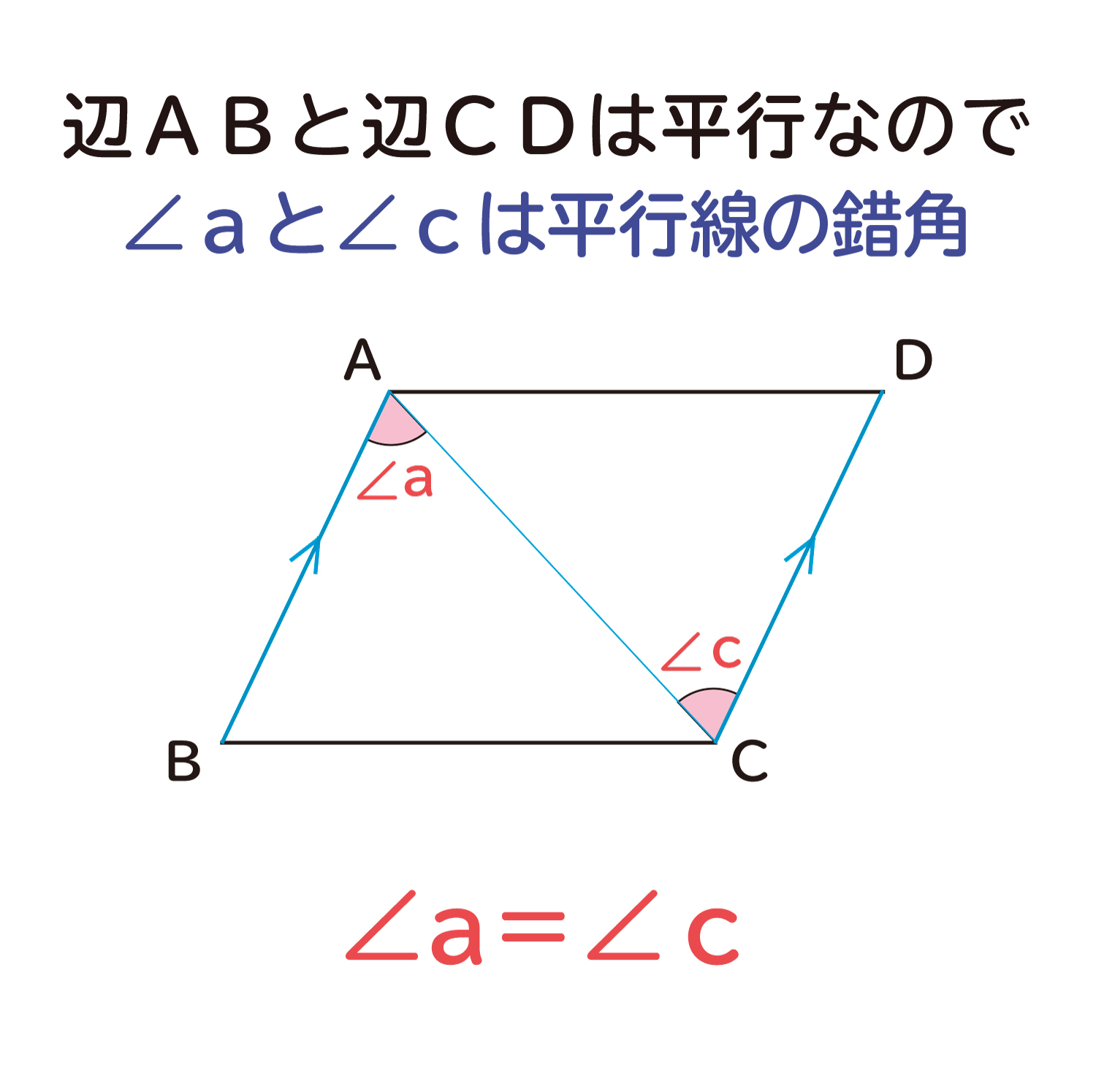
平行四辺形の定義と定理について ① 二組の対辺がそれぞれ平行 ② 〃 等しい ③二組の対角がそれぞれ等しい ④対角線がそれぞれの中点で交わる ⑤一組の対辺が平行でその長さが等しい ②~⑤は①を基に証明できますが、②を定義とし①を証明することは可能なのでしょうか?上のまとめに示したように「平行四辺形」の定義は「2組の向かい合う辺がそれぞれ平行である四角形」すなわち「 ad//bc , ab//dc 」が成り立つ四角形なので,仮定や結論が「平行四辺形」になっているときは「 ad//bc , ab//dc 」に置き換えるとよい この頁では平行線の性質について,証明の進め方 中2の2学期の期末試験には平行四辺形や二等辺三角形などのいろいろな図形が出題されます。 その中でも定義や性質や条件など混乱しやすい用語も多数あります。 ここでいったんわかりやすく整理していきたいと思います。 中2数学の図形に出てくる定義 定義とは用語の意味をはっきり述
平行四辺形の定義はのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  | |
「平行四辺形の定義は」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「平行四辺形の定義は」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「平行四辺形の定義は」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「平行四辺形の定義は」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「平行四辺形の定義は」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「平行四辺形の定義は」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 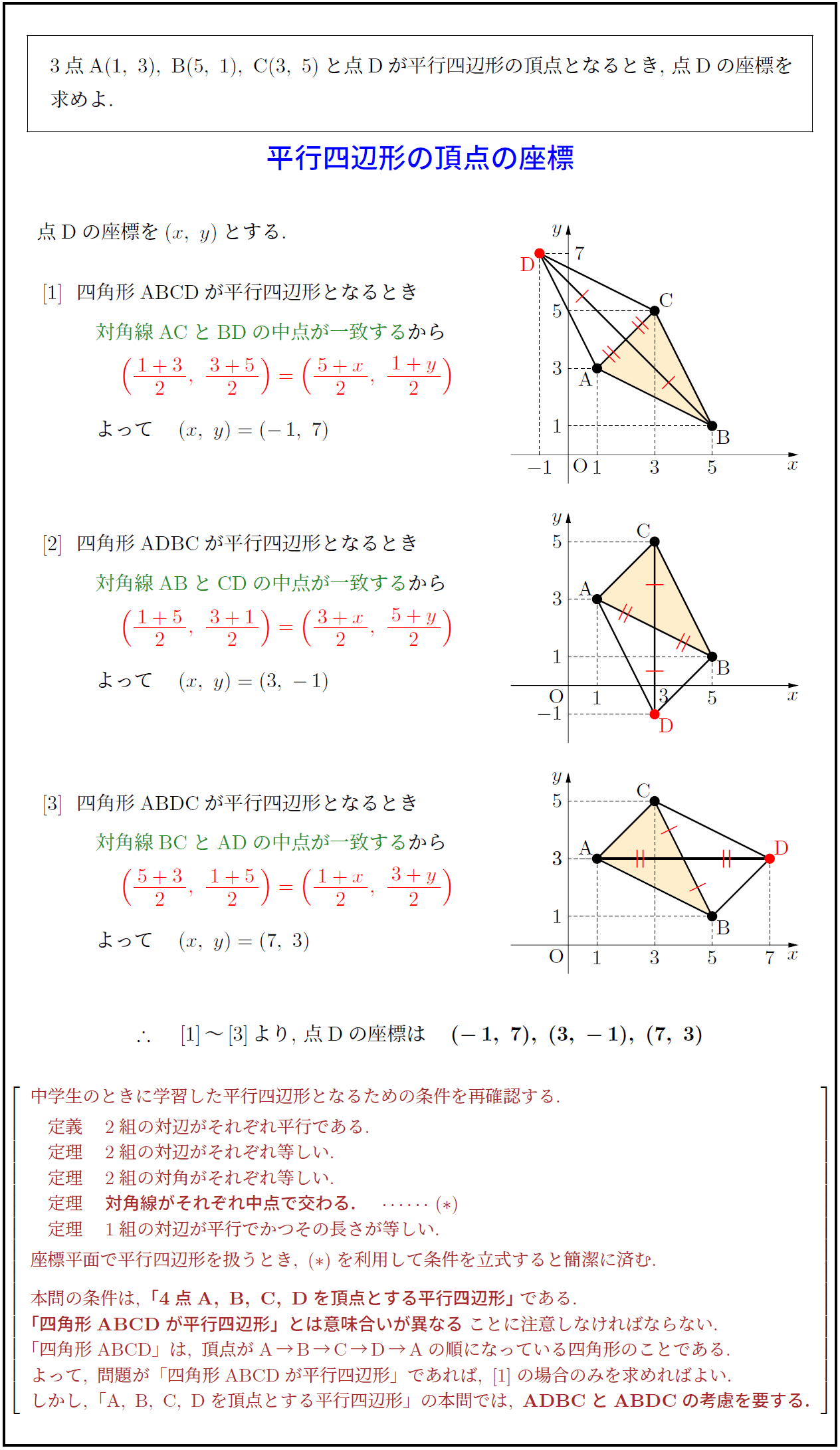 |
 |  | |
 |  |  |
「平行四辺形の定義は」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「平行四辺形の定義は」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「平行四辺形の定義は」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「平行四辺形の定義は」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「平行四辺形の定義は」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |
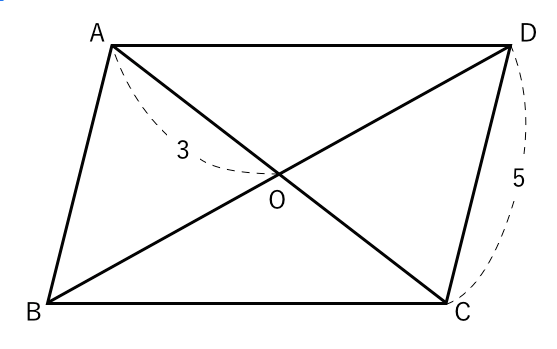
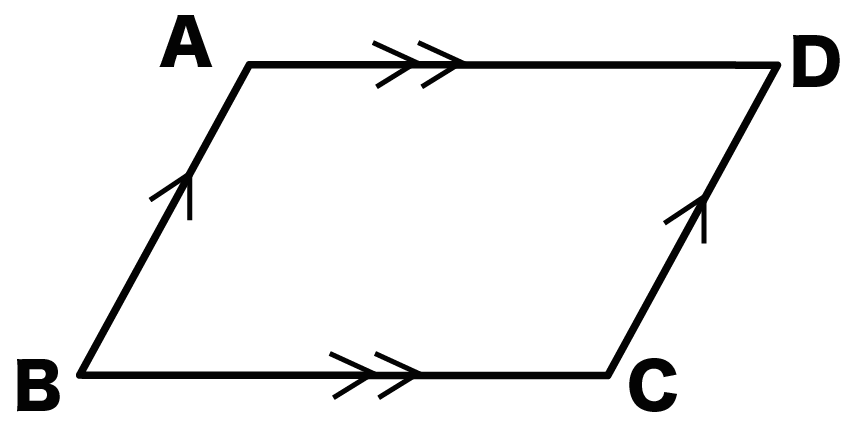
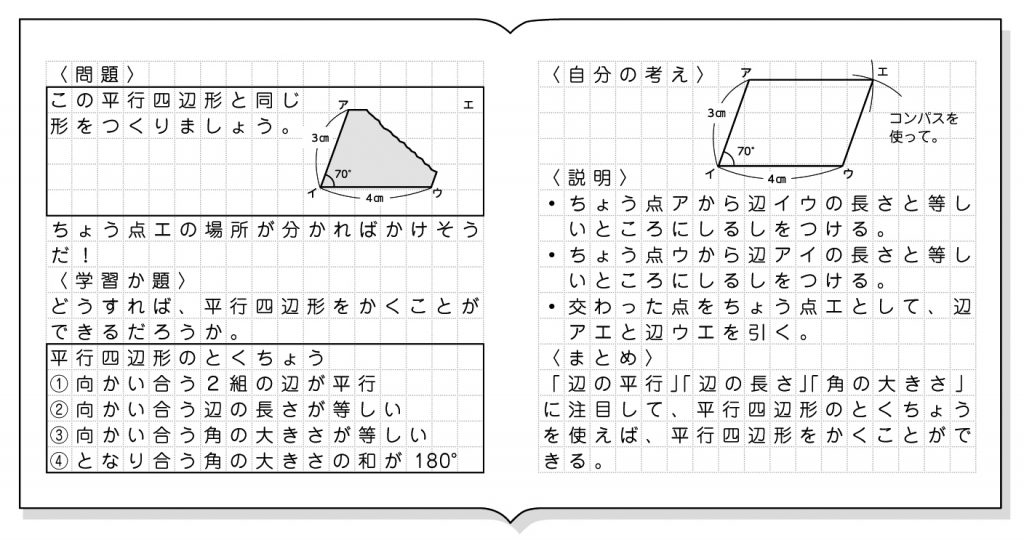
平行四辺形の定義 2組の向かい合う辺が、それぞれ平行な四角形を平行四辺形という。 平行四辺形の性質 内容 (ヒントの図)1 平行四辺形の向かい合う辺は等しい。(証明) 2 平行四辺形の向かい合う角は等しい。(証明) 3 平行四辺形の対角線は、それぞれの中点で交わる。まず平行四辺形の定義は次の通りです. 定義 向かい合う辺がそれぞれ平行である四角形を平行四辺形という. 次のように定義してもかまいません. 定義 四角形abcdが平行四辺形とは ab∥dc,ad∥bc を満たす四角形である. 四角形で,向かい合う辺を対辺,向かいあう角を対角といいます. 現
Incoming Term: 平行四辺形の定義は,



